Badamy problem "żółtej Mleczarki" z wykorzystaniem R i colordistance (część II)

Wprowadzenie

W poprzedniej lekcji poznaliśmy problem “żółtej Mleczarki” oraz podstawy pracy z kolorami w R. Udało nam się wygenerować histogramy, opisujące palety kolorów w poszczególnych reprodukcjach cyfrowych dzieła Vermeera. Analizowaliśmy też na osi 3D dominujące kolory poszczególnych plików. Możemy teraz, bazując na danych o kolorach, zmierzyć różnice między reprodukcjami dobrej i złej jakości.

Cele lekcji

Celem lekcji jest dalsza praktyka pracy w środowisku R. Dzięki metodom z pakietu colordistance wygenerujemy mapę ciepła i wykres drzewiasty (dendrogram), wizualizujące różnice między paletami kolorów reprodukcji Mleczarki Vermeera. Aby taka analiza miała sens, warto porównać je też z reprodukcją wzorcowej jakości, udostępnianą przez Rijksmuseum.

Efekty

• wizualizacja podobieństw i różnic między reprodukcjami cyfrowymi Mleczarki Vermeera,
• umiejętność analizy wykresów drzewiastych (dendrogramów) i map ciepła.

Wymagania

Podobnie jak w poprzedniej lekcji, musimy umieć korzystać z darmowego środowiska programistycznego dla R - serwisu Posit.cloud. Konieczna jest też podstawowa znajomość składni R - warto zapoznać się z wprowadzeniem do pracy z R w Posit.cloud, w razie potrzeby skorzystać z darmowego podręcznika autorstwa Jakuba Nowosada.

Dane do analizy znajdują się na GitHub. W razie problemów z importem do Posit.cloud warto wrócić do opisu z poprzedniej lekcji.

Część merytoryczna

Dzięki dotychczasowej pracy mamy dostęp do zestawu histogramów, wizualizujących dominujące kolory w poszczególnych reprodukcjach Mleczarki. Jak widać z poniższego zestawienia, reprodukcje naprawdę są różnej jakości. Problemem są nie tylko kolory, ale też kadrowanie - ono także wpływa na wyliczanie palety kolorów - warto wziąć to pod uwagę podczas przygotowywania własnego zbioru wizerunków do analizy.

Po lewej stronie widzimy reprodukcję z Rijksmuseum, po prawej - przegląd reprodukcji, które analizowaliśmy w poprzedniej lekcji.

Jeśli mamy już w projekcie utworzonym w Posit.cloud zaimportowane pliki z reprodukcjami, dodajmy do nich jeszcze plik wzorcowy - milkmaid_rijks.png. Jak pamiętamy, wszystkie pliki do analizy umieściliśmy w edytorze programistycznym Posit.cloud w katalogu images. Niech reprodukcja Mleczarki udostępniona przez Rijksmuseum też się tam znajdzie.

Dane z histogramów kolorów

Podobnie jak w poprzedniej lekcji, musimy wygenerować listę danych z histogramów dla wszystkich analizowanych plików. Najpierw tworzymy obiekt images, który będzie zawierał ścieżki do plików:

images <- dir("images", full.names=TRUE)

W efekcie otrzymamy wieloelementowy wektor, w którym znajdziemy ścieżki do wszystkich plików w katalogu images:

 [1] "images/1.png"              "images/100.png"            "images/2.png"             
 [4] "images/3.png"              "images/4.png"              "images/5.png"             
 [7] "images/6.png"              "images/7.png"              "images/8.png"             
[10] "images/milkmaid_rijks.png"

Analizować będziemy dziesięć plików: plik wzorcowy milkmaid_rijks.png, osiem reprodukcji różnej jakości i plik referencyjny 100.png, który na naszych wizualizacjach powinien być radykalnie oddalony od innych plików.

Czas skorzystać ze znanej nam już z poprzedniej lekcji funkcji getHistList, pamiętajmy tylko, żeby mieć w środowisku aktywny pakiet colordistance:

# instalacja pakietu
install.packages("colordistance")
# wczytanie pakietu do środowiska
library(colordistance)

Funkcja getHistList przyjmuje wiele parametrów. Poza ustawieniami parametru lower i lower, odpowiedzialnymi za ignorowanie kolorów tła, oraz wskazaniem na ile koszy (bins) mają zostać wyodrębnione dane o kolorach, ważna dla nas będzie opcja plotting. Ustawmy ją na FALSE - nie będziemy wyświetlać histogramów, potrzebne są nam tylko dane. Parametr n o wartości FALSE oznacza, że analizujemy wszystkie piksele z analizowanych grafik.

Zwróćmy uwagę, że FALSE wpisujemy bez cudzysłowów. To wektory logiczne, których wartości mogą przyjmować wyłącznie kilka wartości: TRUE, FALSE i NA, oznaczająca brak zdefiniowanej wartości (NA nie jest ani prawdą, ani fałszem).

cls <- getHistList(images, n = FALSE, bins=c(2, 2, 2), lower=NULL, upper=NULL, plotting=FALSE, pausing=FALSE)

Wynik działania funkcji zapisaliśmy do obiektu cls. To lista. Listy to klasy obiektów R, które pozwalają na przechowywanie różnych rodzajów danych (tekstowych, logicznych, ramek danych czy innych list). W listach korzystać możemy z operatora $, który pozwala na szybkie wskazanie wybranego elementu listy. Wpisanie takiego polecenia:

cls$milkmaid_rijks

wyświetli nam zawartość ramki danych z danymi na temat dominujących kolorów jednego z analizowanych plików:

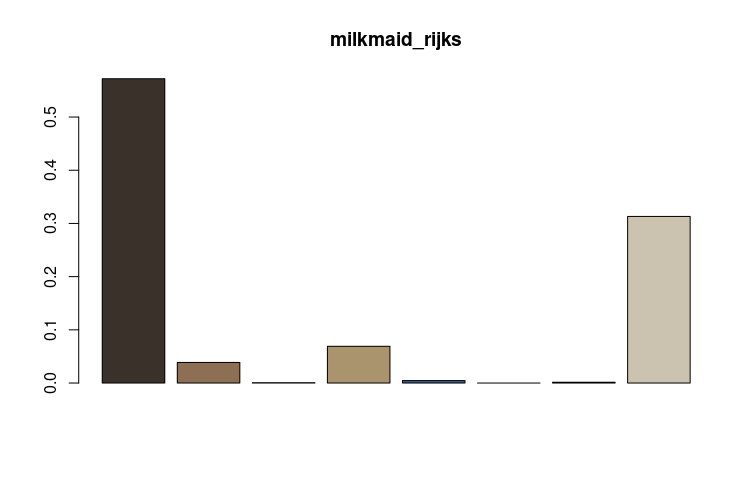
$milkmaid_rijks
          r         g         b          Pct
1 0.2269861 0.1940903 0.1698912 0.5720756032
2 0.5538118 0.4403769 0.3284896 0.0387845758
3 0.4784314 0.5372549 0.4274510 0.0006843605
4 0.6662203 0.5793214 0.4310356 0.0690830814
5 0.2166270 0.3647059 0.5566936 0.0046163226
6 0.7500000 0.2500000 0.7500000 0.0000000000
7 0.3910640 0.5441337 0.6426872 0.0015180360
8 0.7969949 0.7656331 0.6886053 0.3132380206

Widzimy tutaj prosty układ tabeli (kolumny i wiersze). Tego typu dane wygenerowaliśmy dla każdego obrazka w katalogu images. Pierwsze trzy kolumny to współrzędne każdego klastra, a ostatnia kolumna reprezentuje względną wielkość każdego klastra jako proporcję (relatywną do liczby analizowanych pikseli w pliku). Wyobrażmy sobie te klastry jako punkty na w przestrzeni 3D. Kolejne kolumny wskazują na umiejscowienie tych punktów na osiach kolorów podstawowych (czerwonego, zielonego i niebieskiego). Wartości wierszy z czwartej kolumny opisują wielkość danego punktu.

Korzystają z operatora $, który działa także dla kolumn ramek danych, możemy wyświetlić wartości tej kolumny:

cls$milkmaid_rijks$Pct

Jeśli je zsumujemy, dadzą 1 (100%) - to wartości relatywne.

> sum(cls$milkmaid_rijks$Pct)
[1] 1

Porównajmy to z histogramem naszego pliku wzorcowego. Aby go wygenerować, skorzystajmy z funkcji getImageHist:

h0 <- getImageHist("images/milkmaid_rijks.png", n = FALSE, bins=c(2, 2, 2), lower=NULL, upper=NULL)

W palecie dominuje kolor ciemnobrązowy (w tym koszu znalazło się ponad 57 proc. wszystkich pikseli analizowanego pliku):

Jak porównać histogramy?

W wykorzystywanym przez nas pakiecie colordistance skorzystać możemy z metody porównywania rozkładów danych, jaką jest earth mover’s distance (EMD).

Odległość Earth Mover’s (EMD) jest miarą podobieństwa między dwoma rozkładami (np. histogramami) danych. Nasze histogramy reprezentują rozkłady częstości występowania kolorów w obrazie. Przy użyciu EMD możemy porównać te histogramy, obliczając minimalny koszt transformacji jednego rozkładu w drugi. W trójwymiarowej przestrzeni kolorów jest to ilość pracy potrzebna do przeniesienia pikseli z jednego obrazu, aby dopasować się do tych z innego obrazu. Piksele różnych obrazów mogą znajdować się w innych miejscach osi kolorów, np. jeśli w jednym obrazie dominuje kolor jasnożółty, a w drugim żółtozielony. Zbiory tych pikseli mogą też różnić się wielkością - można zobaczyć to na przygotowanej przez nas poprzednio interaktywnej wizualizacji. Im dalej od siebie znajdują się piksele w przestrzeni kolorów lub im większa jest dysproporcja rozmiarów między klastrami, tym większa będzie odległość EMD. EMD wykorzystuje się powszechnie w maszynowej analizie obrazu.

Aby wyliczyć EMD dla każdej pary naszych histogramów, skorzystajmy z funkcji getColorDistanceMatrix:

cls_emd <- getColorDistanceMatrix(cls, method="emd", plotting=FALSE)

Tak prezentują się dane o EMD dla obrazka wzorcowego milkmaid_rijks:

1                  0.06415066
100                0.77891481
2                  0.12250402
3                  0.08548102
4                  0.23895589
5                  0.08162014
6                  0.11993571
7                  0.03547552
8                  0.24158143
milkmaid_rijks             NA

Widać już, jakie reprodukcje są najbardziej zbliżone do reprodukcji wzorcowej 😎. Pamiętajmy, że w języku R, NA oznacza wartość brakującą (nieokreśloną), która może występować w danych, gdy informacja jest nieobecna lub niezdefiniowana. W naszym przykładzie to oczywiste - nie można obliczyć EMD dla tego samego rozkładu danych.

Udało się nam skwantyfikować różnice między reprodukcjami Mleczarki Vermeera: zamiast opisywać je niezbyt konkretnymi pojęciami czy nazywać kolory we własny, subiektywny sposób, wygenerowaliśmy dane o tych różnicach. Teraz czas je zwizualizować, żeby od razu było wiadomo, jakie reprodukcje są najlepszej jakości.

Porównywanie kolorów reprodukcji - mapa ciepła

Zauważmy, że generując EMD dla zbioru naszych reprodukcji funkcją getColorDistanceMatrix, parametr plotting ustawiliśmy na FALSE. Zmieńmy jego wartość na TRUE, aby wygenerować wykres mapy ciepła (heatmap):

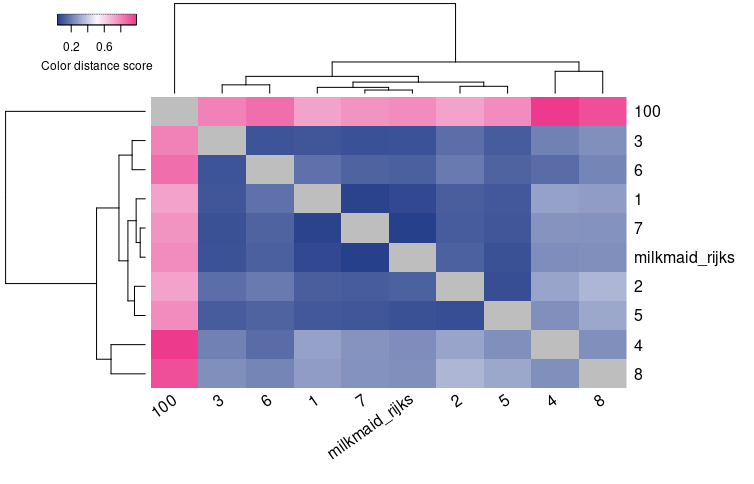
cls_emd_viz <- getColorDistanceMatrix(cls, method="emd", plotting=TRUE)

W efekcie otrzymamy wizualizację porównującą kolory wszystkich plików:

Jak interpretować mapę ciepła?

• zwrócić uwagę na kolory - określają one wartość EMD, czyli skwantyfkowaną różnicę między paletami kolorów naszych plików. Uwaga: kolory wykorzystane w wykresie nie mają nic wspólnego z kolorami palet analizowanych reprodukcji, są jedynie narzędziem wizualizacji,
• zrozumieć znaczenie kolorów dzięki legendzie. Mapa ciepła posiada legendę (Color distance score), która objaśnia, jakie wartości odpowiadają poszczególnym kolorom na mapie. EMD przyjmuje wartość od 0 do 1, im bardziej różowy (fioletowy) kolor, tym wartość EMD jest większa,
• zauważyć zmienność danych (kolorów) w przestrzeni. Analizujmy wybrane pary reprodukcji.

Zacznijmy od pliku 100.png, który jest naszym plikiem referencyjnym (przedstawia dwukolorową szachownicę). Na wykresie widać wyraźnie, że w punkcie wspólnym dla tego pliku i innych plików ze zbioru, wartości EMD są najwyższe. Widać też, że wszystkie pozostałe pliki mają ze sobą więcej wspólnego niż jakikolwiek plik z plikiem 100.png. Żadne z par plików od 1.png do pliku wzorcowego milkmaid_rijks.png nie mają EMD większej niż 0.5 (kolory niebieskie), EMD dla dowolnej pary pliku 100.png i pliku reprodukcji mają powyżej 0.5 (kolory różowe).

A jak znaleźć reprodukcję najgorszej jakości? Zobaczmy, dla jakiej pary pliku wzorcowego i dowolnego pliku (od 1.png do 10.png) wartości EMD są najwyższe. Im bardziej jasny niebieski, tym wartość EMD wyższa - tak jest dla par pliku wzorcowego z plikiem 4.png i 8.png. Rzut oka na reprodukcje potwierdza tę analizę.

W porównaniu ze wzorcową reprodukcją z Rijksmuseum (po lewej), reprodukcja 4.png jest zbyt ciemna (zwróćcie uwagę na cienie na ścianie), a kolory ubrania mleczarki zbyt intensywne:

W przypadku 8.png różnica polega na zbytnim rozjaśnieniu całego obrazu:

Najmniejszą odległość od pliku wzorcowego ma plik 7.png (to nieco ponad 0.03):

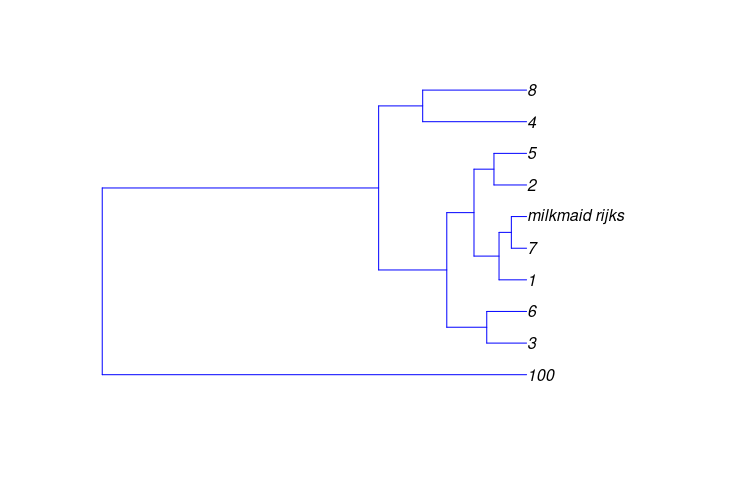
Na wygenerowanej przez nas mapie ciepła widać też klastry plików, uszeregowanie hierarchicznie. Widzimy np., że plik 7.png jest w tym samym klastrze co plik wzorcowy. Również plik 1.png wydaje się być porównywalnej jakości. Taka wizualizacja uszeregowania danych to dendrogram - diagram w kształcie drzewa. W naukach bilologicznych dendrogramy wykorzystywane są jako narzędzie przedstawiania zależności między gatunkami organizmów, w naukach humanistycznych powszechnie wykorzystuje się go w stylometrii, np. w badaniach autorstwa.

Grupowanie reprodukcji pod kątem jakości - dendrogram

Pakiet colordistance umożliwia wygenerowanie dendrogramu z analizowanych danych.

# generujemy dendrogram na podstawie colorDistanceMatrix (parametr plotting = FALSE)

cls_emd_tree_data <- getColorDistanceMatrix(cls, method="emd", plotting=FALSE)

cls_emd_tree <- exportTree(cls_emd_tree_data, 'milkmaids_tree.newick')

W ten sposób zapiszemy w naszym projekcie plik milkmaids_tree.newick. Format .newick jest szeroko stosowany w naukach biologicznych do wizualizacji filogenezy - drogi rozwoju gatunków. Aby wyświetlić plik drzewa, zainstalujmy pakiet ape i skorzystajmy z funkcji read.tree i plot.tree:

# instalujemy pakiet i wczytujemy go do środowiska
install.packages("ape")
library(ape)
# wyświetlamy dendrogram
plot.phylo(read.tree('milkmaids_tree.newick'), edge.color = "blue")

Udało się nam wygenerować wykres pokazujący relacje analizowanych przez nas reprodukcji Mleczarki z plikiem wzorcowym i plikiem referencyjnym:

Przygotowywanie wykresu jest tutaj zgodne z ideą gramatyki wizualizacji, możemy więc zmieniać estetykę wykresu, a nawet rodzaj generowanego drzewa. Więcej informacji znajdziemy w dokumentacji funkcji.

Podsumowanie

Z punktu widzenia humanistyki kolor to przede wszystkim kod kulturowy, nie do końca definiowalny, trudny do porównywania, wymagający subiektywnych ocen. Pakiet colordistance udostępnił nam narzędzia do tego, aby w pewien sposób zobiektywizować kolory i przygotować statystyczne porównanie jakości reprodukcji cyfrowych wybranego dzieła. Dzięki takiemu podejściu przestrzeń kolorów i obrazów może być analizowana w zdystansowany sposób (distant reading) na dużych zbiorach danych.

Warto zwrócić uwagę na to, że korzystaliśmy z narzędzi wypracowanych i przeznaczonych dla dziedzin dalekich od humanistyki (biologia ewolucyjna). Odpowiednio użyte mogą one jednak przydać się także w zastosowaniach badań i analiz kulturowych - metody przetwarzania i analizy danych mogą tu być podobne, inne są już interpretacje. Dobrze myśleć, że możemy swobodnie korzystać z takich narzędzi i mamy pełną swobodę w dostosowywaniu ich do własnych celów.

Pamiętajmy o problemie “żółtej Mleczarki” opracowując plany publikowania zbiorów cyfrowych w naszych instytucjach.

Wykorzystanie metod

Użyta przez nas do porównywania histogramów miara EMD jest powszechnie wykorzystywana w analizie obrazu. Przykładowo, w opublikowanej w 2020 roku pracy Machine Learning Based Analysis of Finnish World War II Photographers wykorzystano EMD w analizie 160 tys. zdjęć historycznych ze zbiorów fińskiego archiwum fotografii wojennej. Wykorzystano tę miarę także w analizie zachowania zwiedzających w przestrzeni muzeum i badaniu ich relacji z obiektami.

Pomysł na warsztat

Obie lekcje mogą zostać wykorzystane do przeprowadzenia warsztatu z R. Poza tym kontekstem można zainteresować się mapami ciepła i dendrogramami jako metodami wizualizacji danych i w ramach warsztatu przygotować ćwiczenia na ten temat. Nie muszą to zresztą być ćwiczenia wymagające korzystania z komputerów - wystarczy kartka i kolorowe mazaki. Mapa ciepła i dendrogram może być ciekawym schematem rozrysowania relacji między postaciami wybranej powieści albo profilu programów politycznych XIX-wiecznych partii politycznych. Przygotowując takie ćwiczenie należy zastanowić się, jakie dane lub cechy mogą być podstawą analizy.